Inference on missing locations in Geostatistics under Preferential Sampling
Conference
64th ISI World Statistics Congress
Format: CPS Abstract
Keywords: missing-values, sampling, stochastic
Session: CPS 17 - Statistical inference
Monday 17 July 4 p.m. - 5:25 p.m. (Canada/Eastern)
Abstract
This paper deals with the inverse problem in Geostatistics in situations where the researcher performs inference about missing locations under a specific type of informative sampling design. Based on the traditional Geostatistical model, one can found in the literature methods for drawing samples from the resulting predictive distribution of the missing locations considering that the underlying stochastic process of interest is independent of the sampling design, i.e., assuming the sampling design is not preferential. However, in cases where the sampling design is preferential it is necessary to specify a joint distribution for both the stochastic process and the sampling design and a common choice is to assume log-Gaussian Cox processes and stationary Gaussian process to deal with this situation. Unfortunately, under preferential sampling, deriving a straightforward way to obtain the predictive distribution of the missing locations is a complex task. In this paper we present a methodology to obtain the predictive distribution of missing locations under preferential sampling.
Figures/Tables
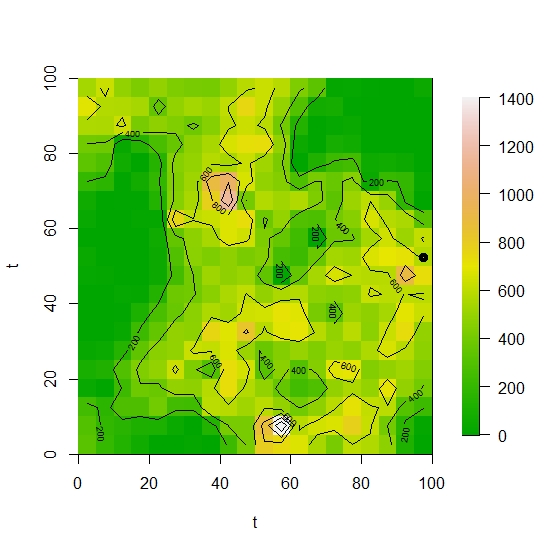
dados_max
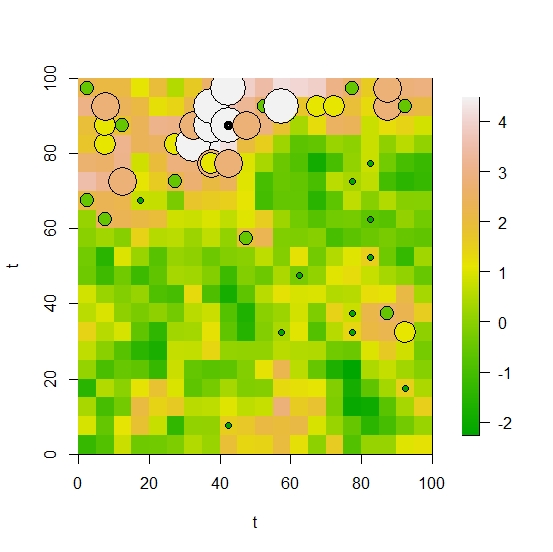
dados_min
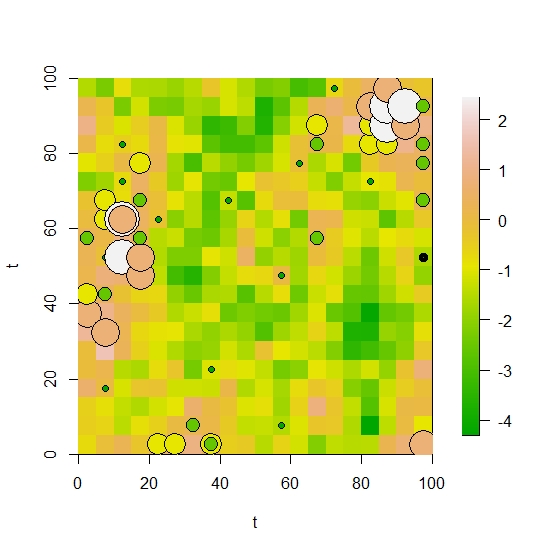
max_NP
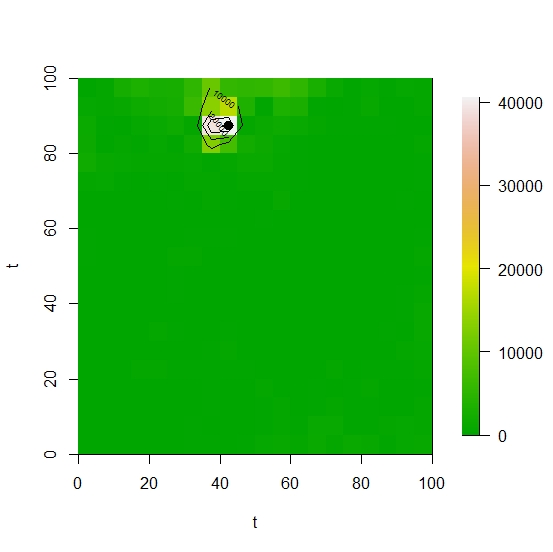
max_PS
min_NP
min_PS