An Aggregate Test for Polynomial Frequency Modulation Using Multitaper Methods
Conference
64th ISI World Statistics Congress
Format: CPS Paper
Keywords: modulation, multitaper, spectrum, time-series
Session: CPS 57 - Statistical testing
Tuesday 18 July 4 p.m. - 5:25 p.m. (Canada/Eastern)
Abstract
We propose a semiparametric multitaper test for the detection of modulated
line components where the modulation is assumed to be created by a polynomial
of degree P. This test is based on an aggregation of F-tests described in [1]
that are based on the multitaper framework [2]. The multitaper method is
a robust estimator for the spectral density of a time series, with significant
performance gains over classical approaches such as the periodogram or direct
spectral estimators. The method uses a family of orthogonal tapers, providing
consistency, reducing variance and controlling broad-band bias in the estimators.
Although any arbitrary sets of weights could be used as tapers, by far the
most commonly used in practice are the Discrete Prolate Spheroidal Sequences
(DPSSs). These sequences are found as the solution to the problem of maxi-
mization of energy concentration in a chosen bandwidth [4]. While optimal in
that sense, one downside of using DPSS tapers is the required computation time
for estimating solutions when both the time series length N and the number of
tapers K are large. This did not pose a problem for the F-test described in
Blanchette et al. [1] but is more noticeable in our new aggregated test due to
the increased computational complexity. An alternative taper scheme is sinu-
soidal tapers [3], which are an approximation of the minimum bias tapers of
the spectral estimator, having very high computational efficiency due to their
closed form. Another advantage of the sine tapers is the ability to downweight
specific regions of the bandwidth: this is useful for providing a mechanism for
controlling Type I error in our new aggregated test.
The aggregated polynomial F-test we propose uses multiple iterations of
different sinusoidal tapers along with a weighting scheme to help control Type I
error, while also reducing the total computation time that would be required if
using the DPSSs. In this work, we derive an approximate distribution for this
aggregated test and discuss a simulation study of its performance. In addition,
comparisons of our new aggregated test against the F-tests in [1] are conducted.
References
[1] Blanchette, K., Burr, W., & Takahara, G. (2021). An F-test for polynomial
frequency modulation. ICASSP, IEEE International Conference on Acous-
tics, Speech and Signal Processing - Proceedings, 2021-June, 5010–5014.
https://doi.org/10.1109/ICASSP39728.2021.9414209
[2] Thomson, D. J. (1982). Spectrum Estimation and Har-
monic Analysis. Proceedings of the IEEE, 70(9), 1055–1096.
https://doi.org/10.1109/PROC.1982.12433
[3] Riedel, K. S., & Sidorenko, A. (1995). Minimum bias multiple taper spec-
tral estimation. IEEE Transactions on Signal Processing, 43(1), 188–195.
https://doi.org/10.1109/78.365298
[4] Slepian, D. (1978). Prolate Spheroidal Wave Functions, Fourier Analysis,
and Uncertainty—V: The Discrete Case. Bell System Technical Journal,
57(5), 1371–1430. https://doi.org/10.1002/J.1538-7305.1978.TB02104.X
Figures/Tables
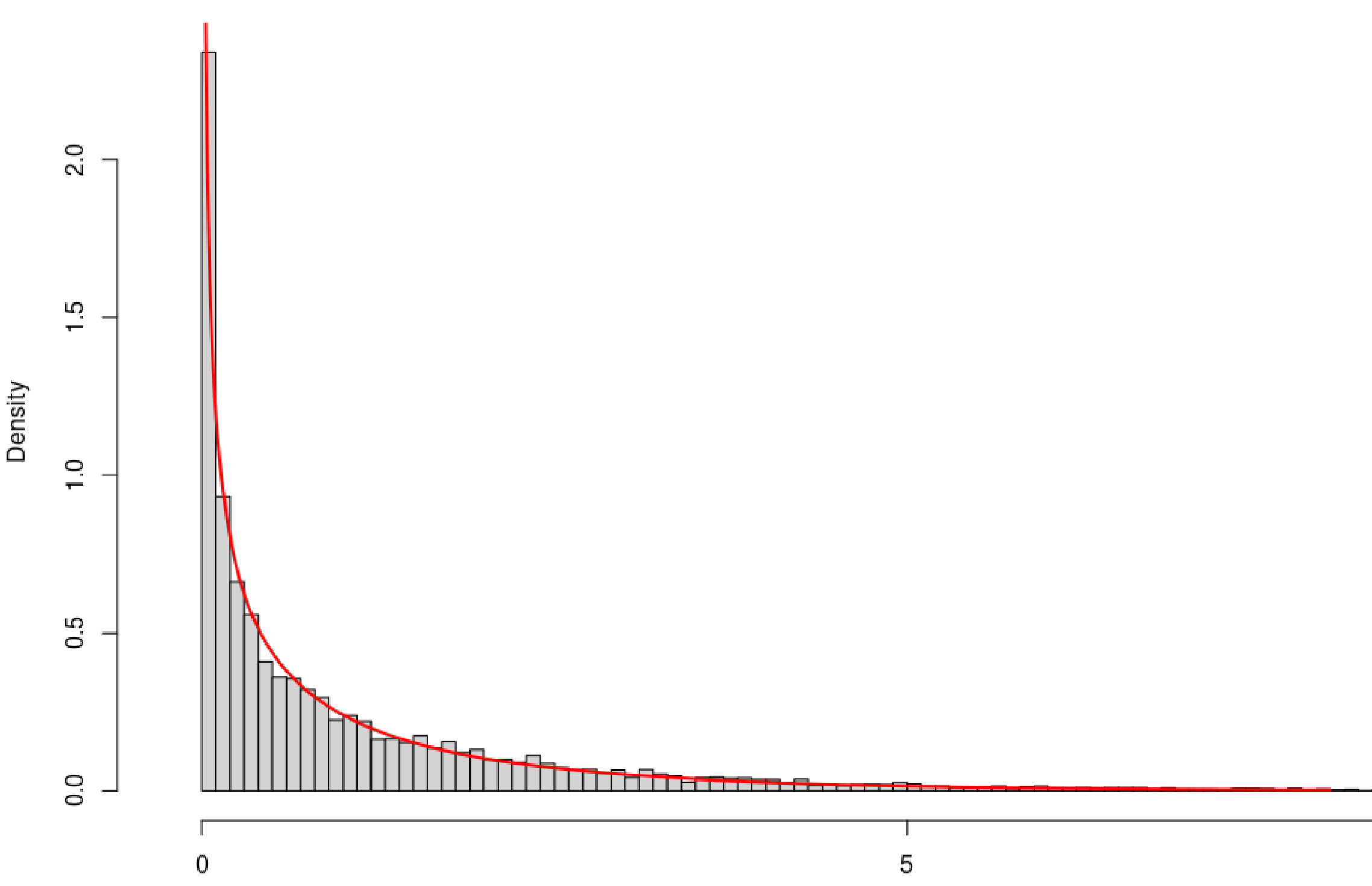
Density Of F4
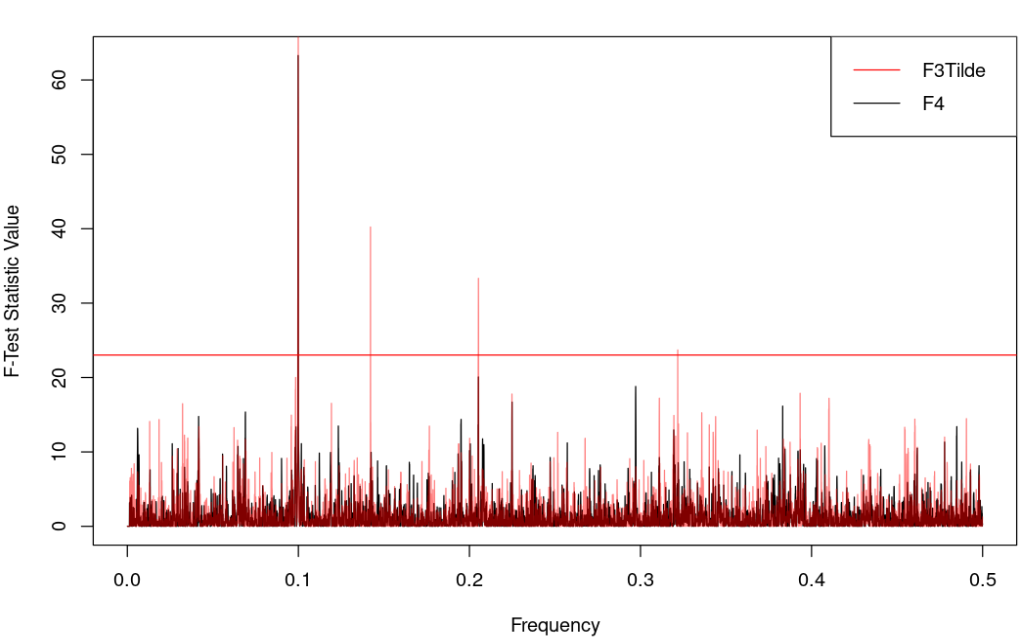
Comparison Of F3Tilde and F4
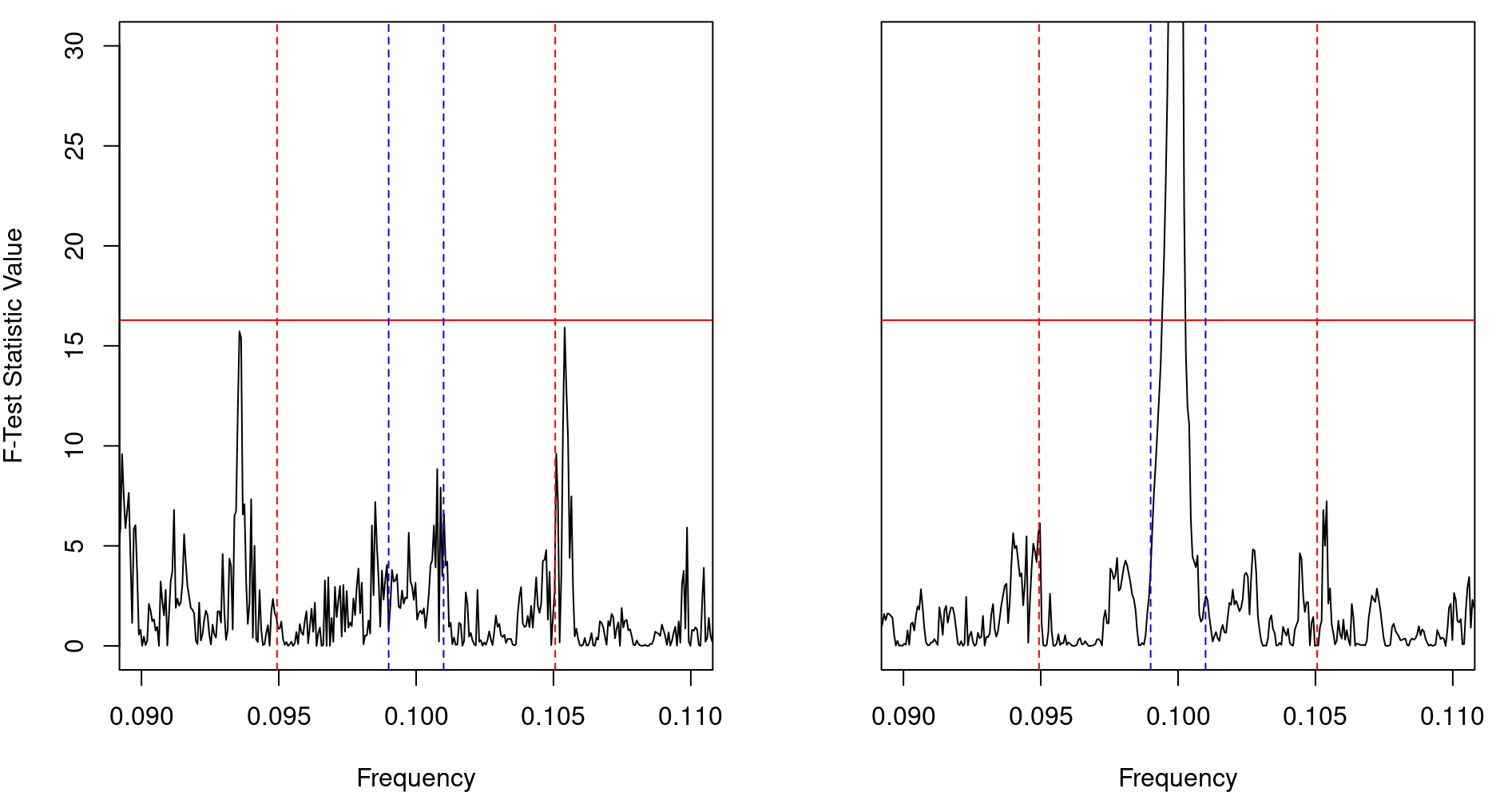
Comparison of F3Tilde and F4 for K = 20
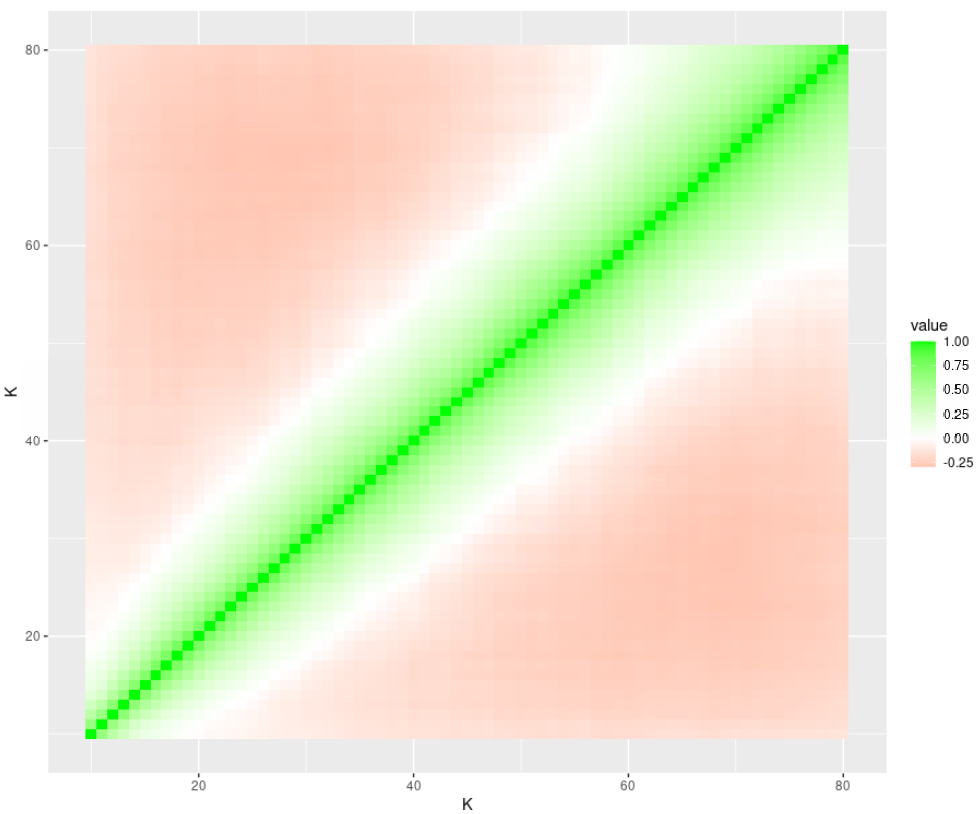
Correlation Estimate for F4
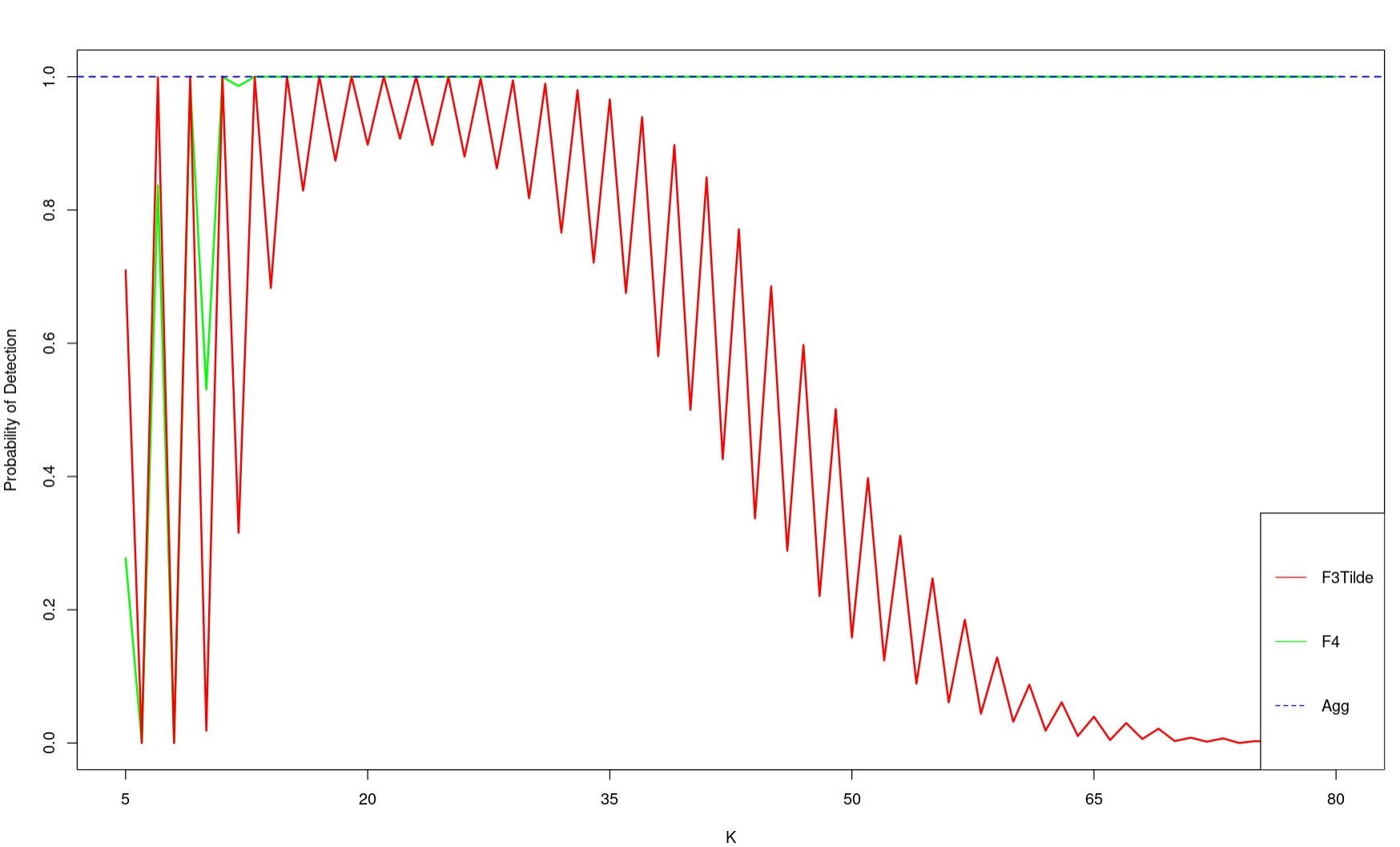
Probability of detection for modulation bandwidth 0.0005, comparing F3Tilde and F4
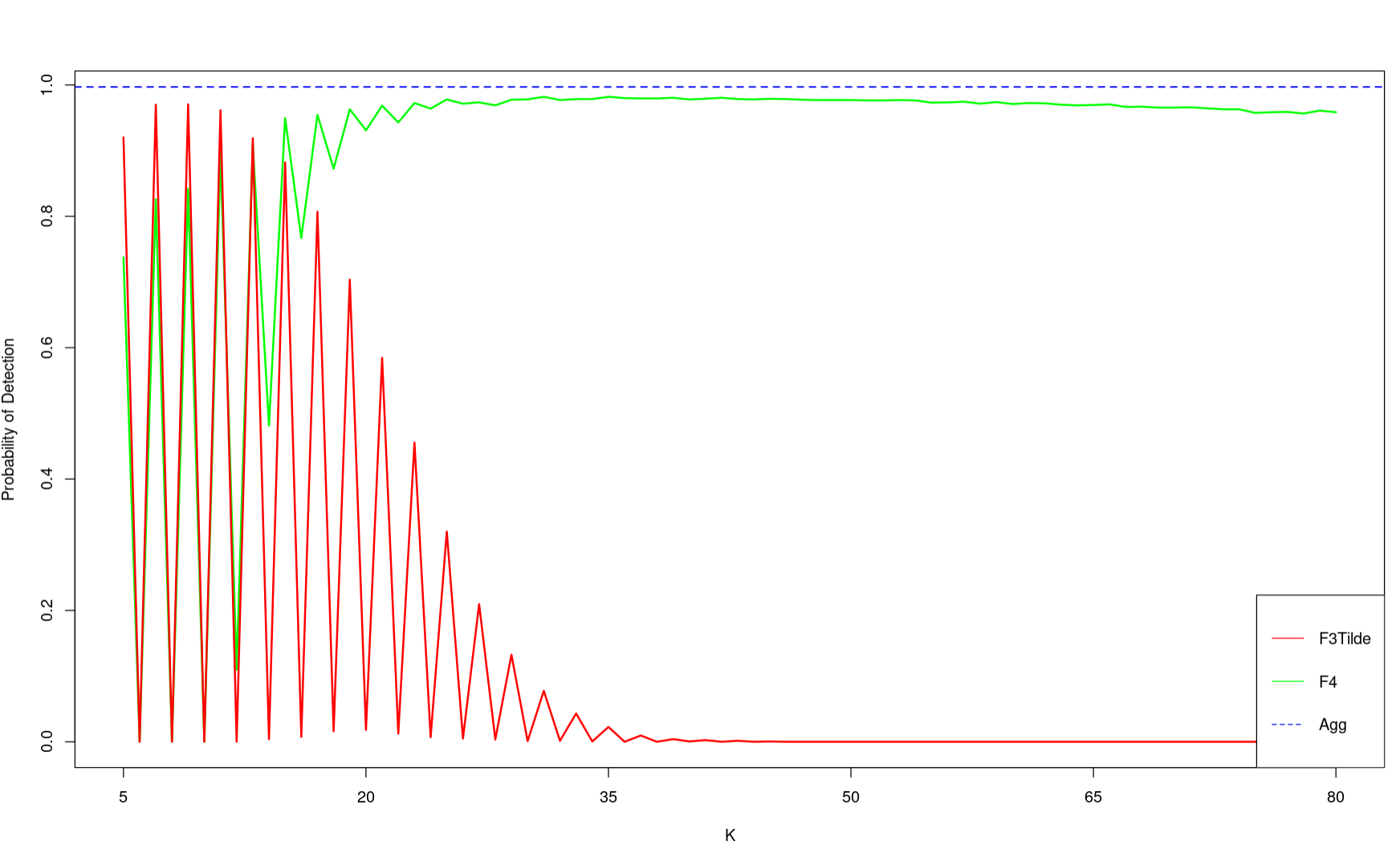
Probability of detection for modulation bandwidth 0.001, comparing F3Tilde and F4