A useful parametric specification to model epidemiological data: revival of the Richards’ curve
Conference
64th ISI World Statistics Congress
Format: CPS Abstract
Keywords: bayesian_model, dispersion models for count data, epidemiology, growth, maximum likelihood
Session: CPS 75 - Statistical modelling IV
Wednesday 19 July 8:30 a.m. - 9:40 a.m. (Canada/Eastern)
Abstract
A useful parametric specification for the expected value of epidemiological processes is revived, and its statistical and empirical efficacy are explored. The Richards' curve is flexible enough to adapt to several growth phenomena, including recent epidemics and outbreaks.
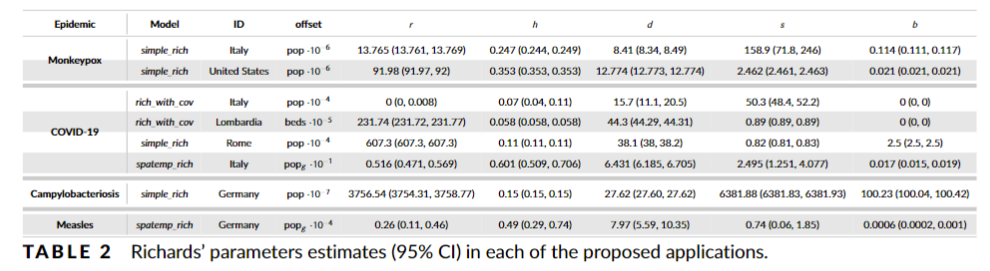
Here, two different estimation methods are described. The first, based on likelihood maximization, is particularly useful when the outbreak is still ongoing and the main goal is to obtain sufficiently accurate estimates in negligible computational run-time. The second is fully Bayesian, and allows for more ambitious modeling attempts such as the inclusion of spatial and temporal dependence, but it requires more data and computational resources. Regardless of the estimation approach, Richards' specification properly characterizes the main features of any growth process (e.g. growth rate, peak phase, etc.), leading to a good fit, while also providing trustworthy short- to medium-term predictions. To demonstrate such flexibility, we show different applications using publicly available data on recent epidemics where the data collection processes and transmission patterns are extremely heterogeneous, as well as benchmark datasets widely used in the literature as illustrative.
Figures/Tables
RichardEstimateMonkeypoxNew_US
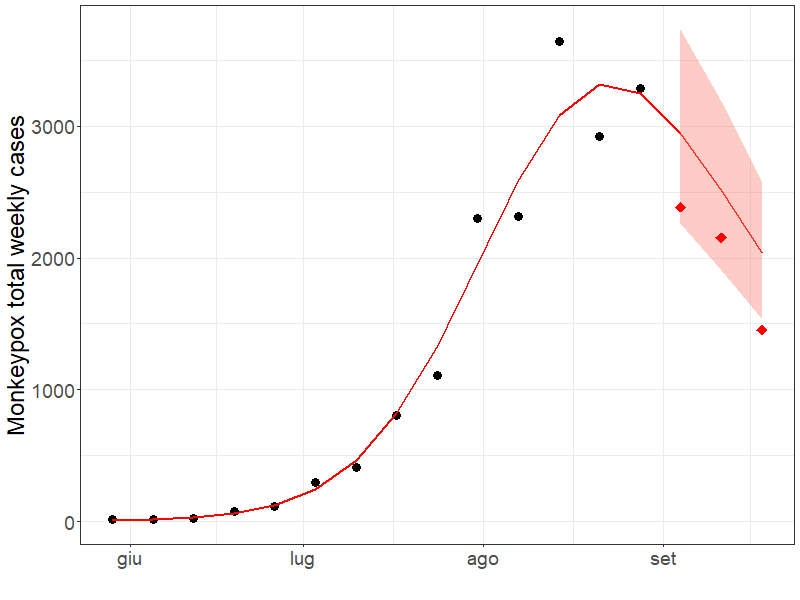
RichardEstimateCOVID_DeceasedItaly
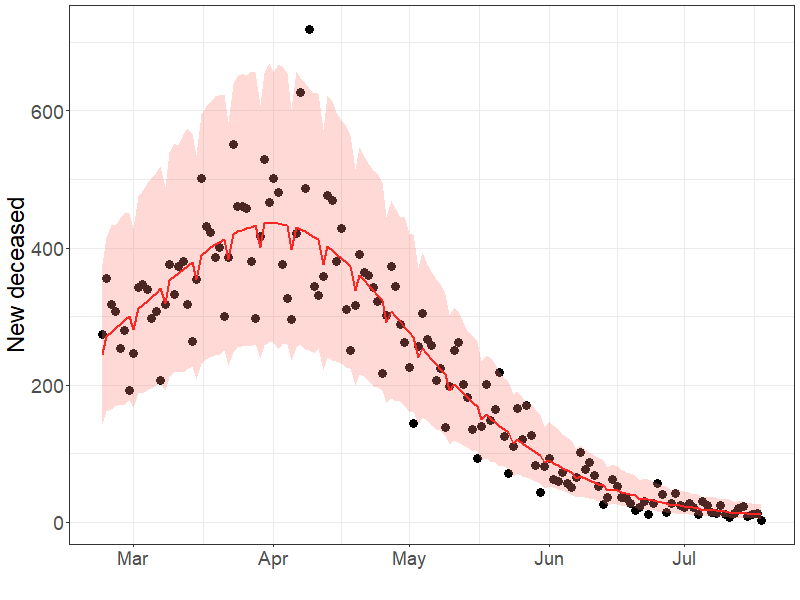
RichEstNationalItaly
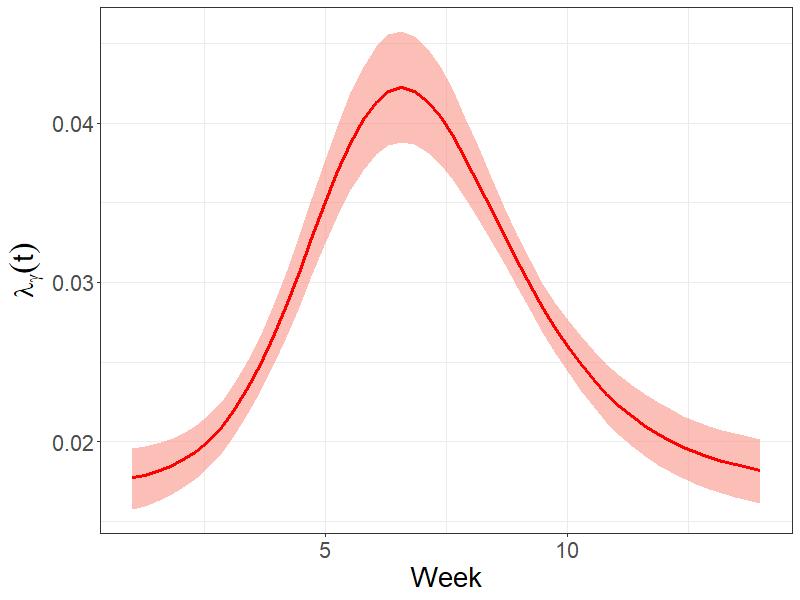
RandomEffects_SpatialCovid
Screenshot (151)

Screenshot (152)